How do we Multiply Exponents?

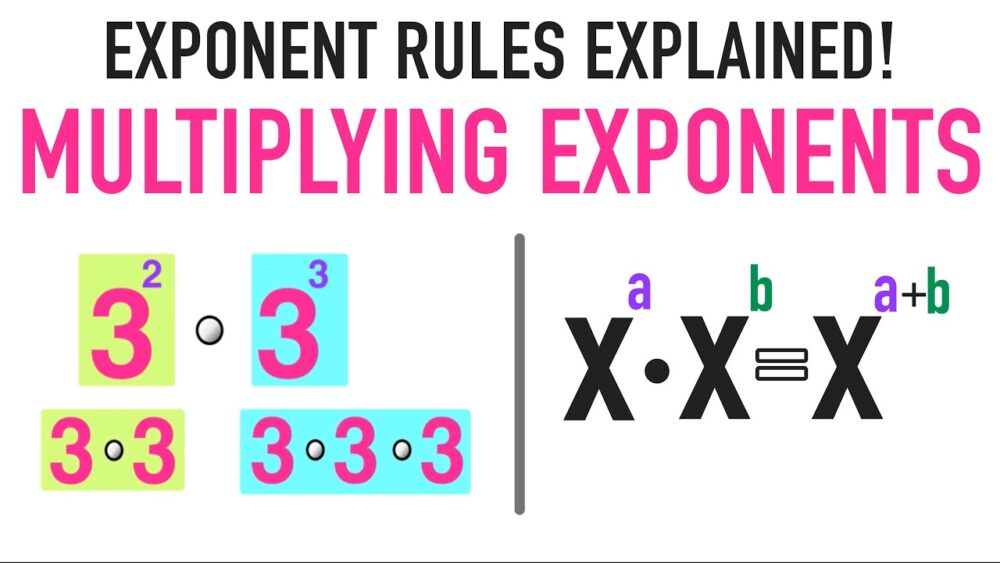
Exponents can be defined as powers or indices. It is used to denote how many times a number is repeatedly multiplied by itself. The general form of an exponential expression is given by bn. b denotes the base, and n denotes the exponent that the base is raised to. Suppose a number is written as 32; this implies that three is multiplied by itself 2 times. We can also say 32 = 3 * 3 = 9. In this article, we learn more about multiplying exponents and other associated concepts.

As performing exponential multiplication forms a crucial part of mathematics, it is necessary for kids to understand the topic clearly. There are several related topics to exponents, such as logarithms, and to solve these problems, kids need to have a solid mathematical foundation. The best way to acquire such knowledge is by joining a coaching institute such as Cuemath. The certified tutors use various resources such as worksheets, workbooks, puzzles, and math games to teach a class. They ensure that a child has fun while learning. Thus, you can turn to a good tutoring institute and master the topic in no time!

Rules of Multiplying Exponents 

1. Product of powers rule: If exponents have like bases, the powers are added.
2. The quotient of powers rules: When dividing like basis, the powers will be subtracted.
3. Power of powers rules: When rising power by another exponent, multiply the powers together. 
4. Power of product rule: Powers will be distributed to all values in a quotient. 
5. Zero power rule: Any base that is raised to zero will become one.
6. Negative exponent rule: Negative exponents can be changed to positive exponents by flipping them into a reciprocal.

Multiplying Exponents with the Same Base

In such a type of multiplication with like bases, the powers are added, i.e., aman = am+n 

E.g. 5253 = 55

Multiplying Exponents With Different Bases

When we multiply exponents with different bases, the bases need to be multiplied. However, it needs to be kept in mind that the value of the exponents remains the same, i.e., anbn = (ab)n  

E.g. 52 32 = 152

If both bases are different and the exponents are of a different value, then the value is computed by finding each number’s value and then multiplying it. 

E.g. 51 32 = 59 = 45

Multiplication of Negative Exponents

For numbers that have negative exponents and the same base, we add the exponents, i.e., a-ma-n = a-(m+n) = a1/(m+n)

E.g. 5-25-3 = 5-5

If the numbers have a different base but the same exponents, we multiply the bases. a-nb-n = (ab)-n 

E.g. 5-2 3-2 = 15-2 

Multiplication of Fractions With Exponents

If the fractions are the same, then the exponents are added. If the base is different, however, the exponents are the same; we multiply the bases.

E.g (5/2)2(5/2)3 = (5/2)5

E.g. (5/3)2(5/2)2 = (25/6)2

Multiplication of Fractional Exponents

If the bases are different, the exponents are added; however, if the bases are different but the fractional exponents are the same, then the bases are added. 

E.g. 43/244/3 = 417/6

E.g. 43/293/2 = 363/2

Multiplication of Roots with Exponents

If the base of two numbers that are in the form of roots is the same, then we add the exponents and the root forms a part of the number.

E.g. (2)5(2)3 =(2)8/2 = (2)4

Conclusion      

As performing exponential multiplication forms a crucial part of mathematics, it is necessary for kids to understand the topic clearly. There are several related topics to exponents, such as logarithms, and to solve these problems, kids need to have a solid mathematical foundation. The best way to acquire such knowledge is by joining a coaching institute such as Cuemath. The certified tutors use various resources such as worksheets, workbooks, puzzles, and math games to teach a class. They ensure that a child has fun while learning. Thus, you can turn to a good tutoring institute and master the topic in no time!